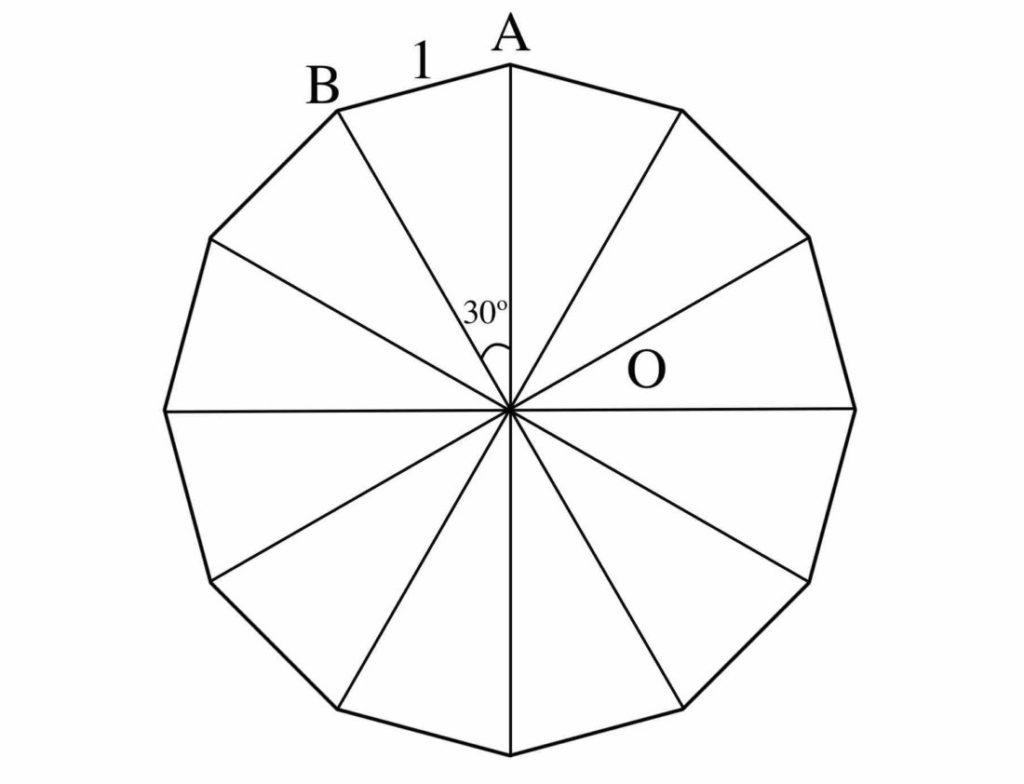
正12角形ですから、図の AOBと合同な二等辺三角形が12個あります。 AOBの面積を求めて12倍すれば良いわけです。 解説 AOBの底辺はRで高さはhであるとし、 hをRで表すことを考える。 ∠AOB=360÷12=30゜正十七角形は作れる ようやくタイトルの話に戻ってきました。 「正十七角形が作れる」すなわち「正十七角形は作図可能である」ということをはじめて示したのは、19 世紀最大の数学者と謳われた「カール・フリードリヒ・ガウス」です。11角形・・・・・「A1」~「A11」に、1、と入力⇒範囲選択⇒グラフウイザード⇒グラフの種類、「レーダー」⇒完了 11角形の数値で右クリック⇒クリアー、続けて 中の直線でF4キー ワッカでF4キー 凡例でF4キー グラフの外枠で右クリック⇒グラフエリアーの書式設定⇒線なし、領域なし、
第3回 基礎作図 基本的な作図法をしっかりと学ぶ 本日の課題 Ppt Download
正12角形 書き方
正12角形 書き方-「正多角形」の意味や性質を理解する。 円の中心の周りの角を等分して正多角形をかく方法を理解する。 円の半径の長さを使って正六角形を作図し,正多角形と円の関係について理解を深 める。 (本時 4, 5/8)前回ゼンタングルで正八角形を書くのにちょっと苦労したので、忘れないうちに正八角形の書き方をまとめておきます。 小学校か中学校の算数?数学?の問題でもありましたね〜(^^;) wwwmgraffiticom 正八角形の書き方 まずは正方形を書きます 次に対角線を書きます 対角線の交点と四角形の頂点


三角比を用いた面積計算をマスターしよう スタディクラブ情報局
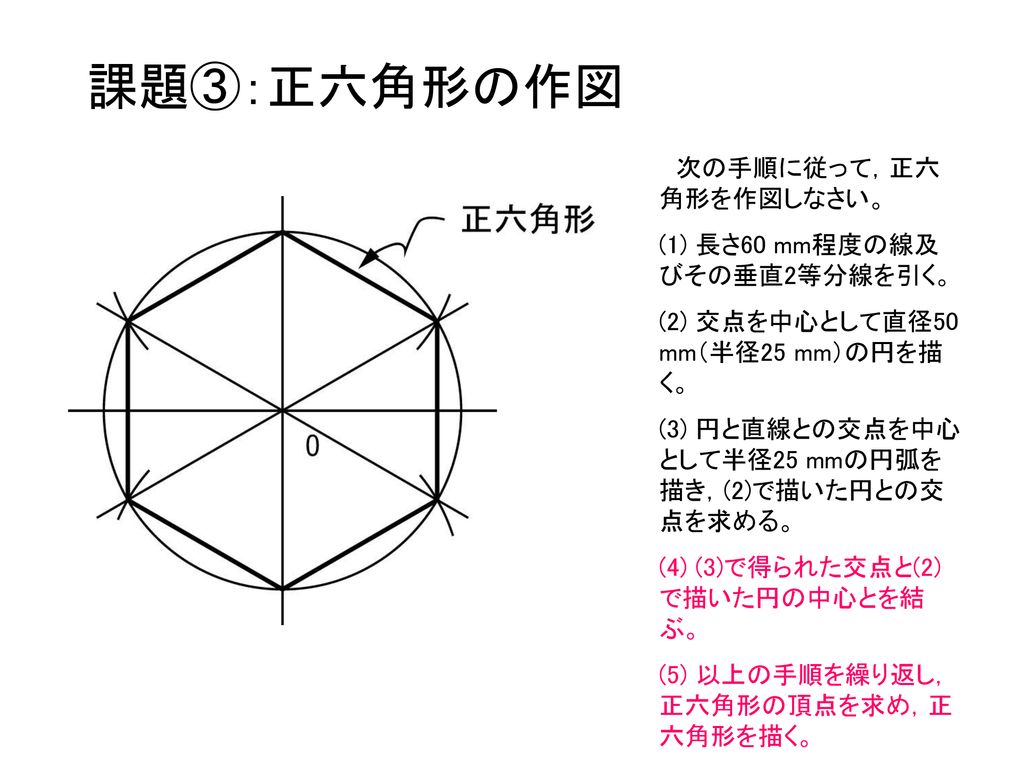
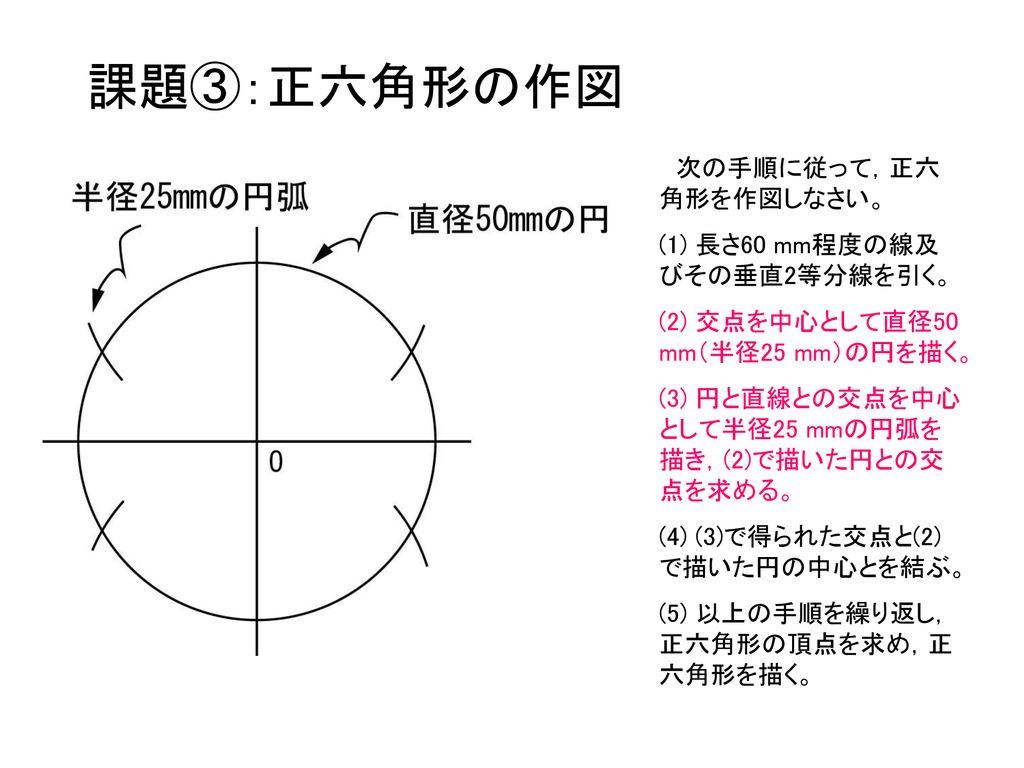
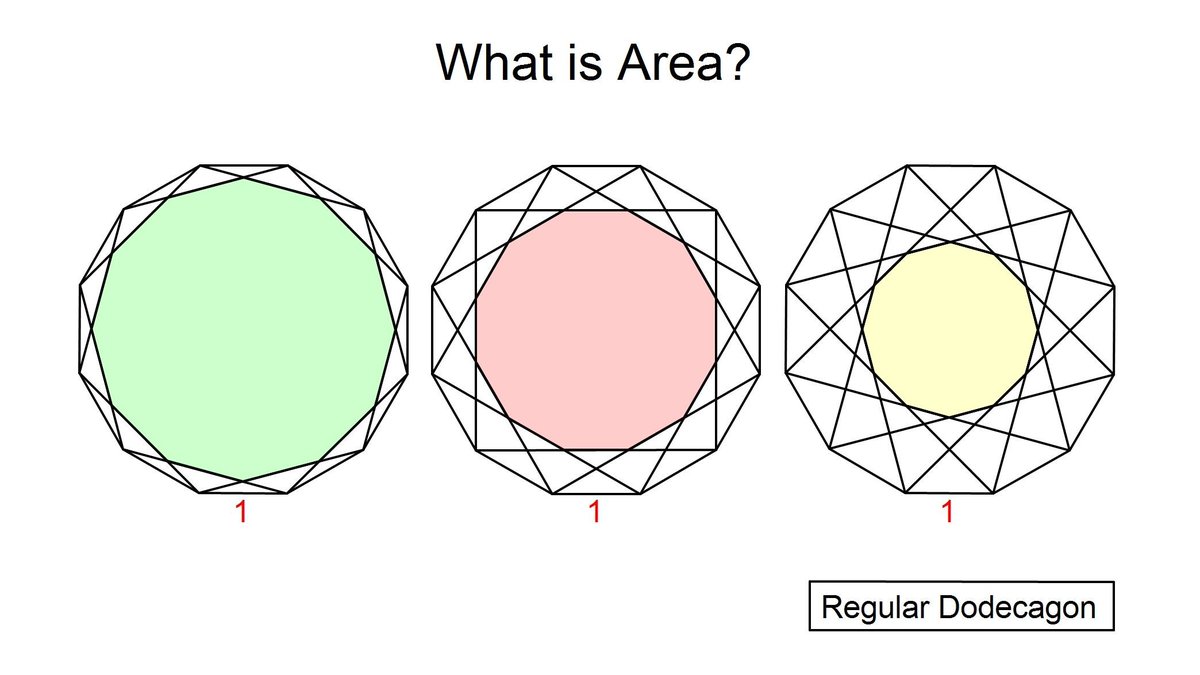
正十二角形においては、中心角と外角は30°で、内角は150°となる。 一辺の長さが a の正十二角形の 面積 Sは S = 3 a 2 cot π 12 = 3 a 2 ( 2 3 ) ≃ a 2 {\displaystyle S=3a^{2}\cot {\frac {\pi }{12}}=3a^{2}\left(2{\sqrt {3}}\right)\simeq a^{2}} となる。一辺が1cmの正十二角形の内側に、1cmの正三角形が12個並んでいます。 このとき、色のついた部分の面積は何cm 2 ですか。 この問題は、下図のように変形することができ、一辺が1cmの正方形6個分になるので、答えは 6cm 2 。(2) 課題③を参考にして,円Oを12等分し,番号0~11をふる。 (3) 円O中心の右に,長さ1 mm直線ABを引く。 (4) ドラフタを使って,点A,Bから垂直線を引く。 (5) 円Oの各点(0~11)から横方向に平行線を引く。 (6) 直線ABを12等分(10mm間隔)し,番号0~11をふる。
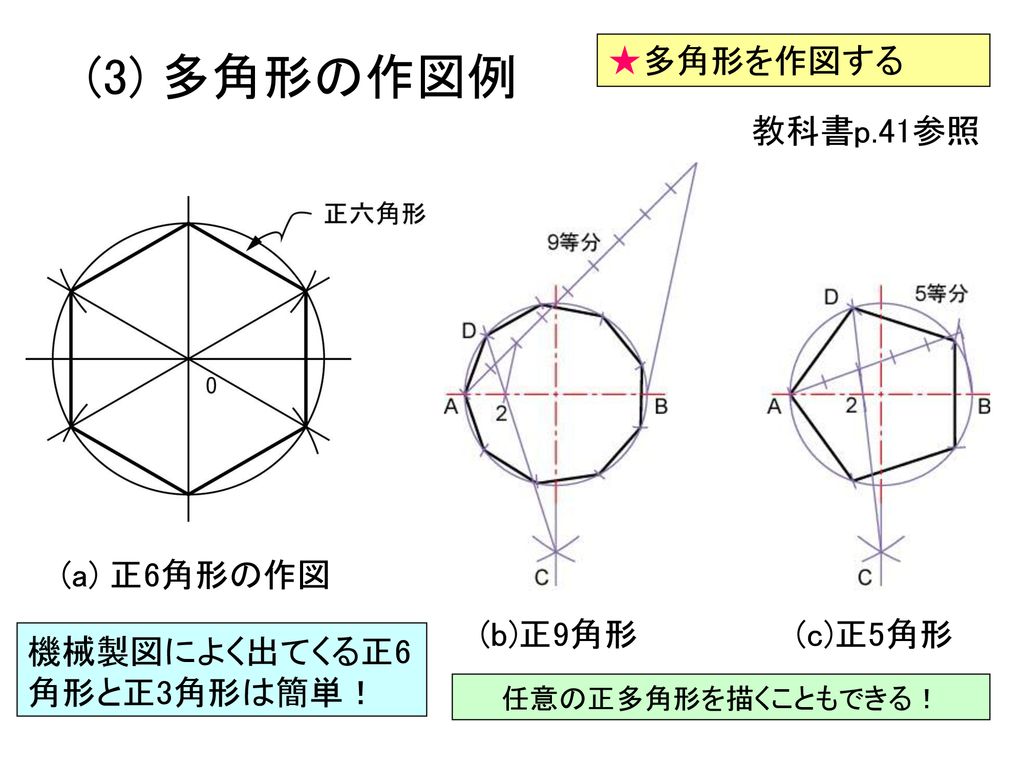
数学的には正解ではない作図法です。 ☆用具:直線定規、コンパス、分度器 (1) 点Oを中心とした円と、点Oを通る直線と、それに直角に交わる垂直線を描く。 (2) 中心の点Oから72度の角度に5本の線を引いて、円と線の交点を結ぶと正五角形の完成。 このページのトップに戻る 「定規とコンパスで作図」目次に戻る メールマガジンに戻る まめ辞典に戻るコンパスも分度器も使わずに定規だけで ・ほぼ五角形 ・およそ星型 を書く方法を紹介します。 以前 「簡単な星の描き方」の記事を書いたのですが、 小学生がいないご家庭ではコンパスや分度器は置いていないと思います。 なので、簡単に「ほぼ五角形」が書ける方法を紹介したいと思い正十二角形の作図 正12角形は、正6角形の外接円と、その一辺の二等分線が交わる点を求める方法で作図します。 正十三角形の作図 正13角形。連結式奇数等分器の部分を6枚使います。十文字の照準線の長い部分を重ねる方がいいと思います。
正十二面体 正五角形が \(12\) 面なので、バラバラのときの辺の数は、 \(5×12=60\) 立体にすると半分になるので、\(60÷2=30\) よって、辺の数は \(30\) 正二十面体 正三角形が \(\) 面なので、バラバラのときの辺の数は、 \(3×=60\) 立体にすると半分になるので、\(60÷2=30\)正n角形の1つの内角は、 中1数学 中3数学 161 中学数学二次関数y=ax2のグラフの書き方がわかる3つのステップFusion360で正二十面体を作る! まずは、一辺が60mmの正五角形を、Fusion360のスケッチで「内接ポリゴン」で描きます。 次に、下に「オフセット平面で」作業面を作り、同じ正五角形を描き180度回転させます。 ポリゴンで正五角形を描く オフセット平面で作業面を作る 正五角形を描いて、180度回転させる 次に頂点となる点をこれまた、上下に書くためにFusion360の



トップ 100 12 かっ けい 写真と画像


十一角形 Wikipedia
正12角形を形成する12個の三角形は、 すべて合同な形 をしていますので、角度や辺の長さはすべて同じになります。 ですので、 ∠AOB=360°÷12=30°となり となります。 ケアレスミスのないように! 最後に忘れないでおいてください! この問題は正12角形の面積を求める問題です。 いま求めたのは三角形AOBの面積なので、これを12倍しなければ答えになりません(6) 正7角形を作図する。 付図33 正7角形の作図 補足付図34に示すように,同様の作図法によって,c1=c7,c2=c8,c5=c10,c6=c12となるように点7,点8,点10,点12を求めれば,様々な正多角形を作図できる。ただし,n=6,12以外は近似法である。 付図34 正多角正六角形の作図 正6角形。書き方はいちばんシンプルですね。 正七角形の作図 正7角形。連結式奇数等分器の部分を3枚使います。 正八角形の作図 正8角形。これは正方形の作図法のなかですでに出来ていました。 正九角形の作図 正9角形。


アルキメデス以来の新種発見 正七角形を使った半正多面体 発想力教育研究所 素数誕生のメカニズム
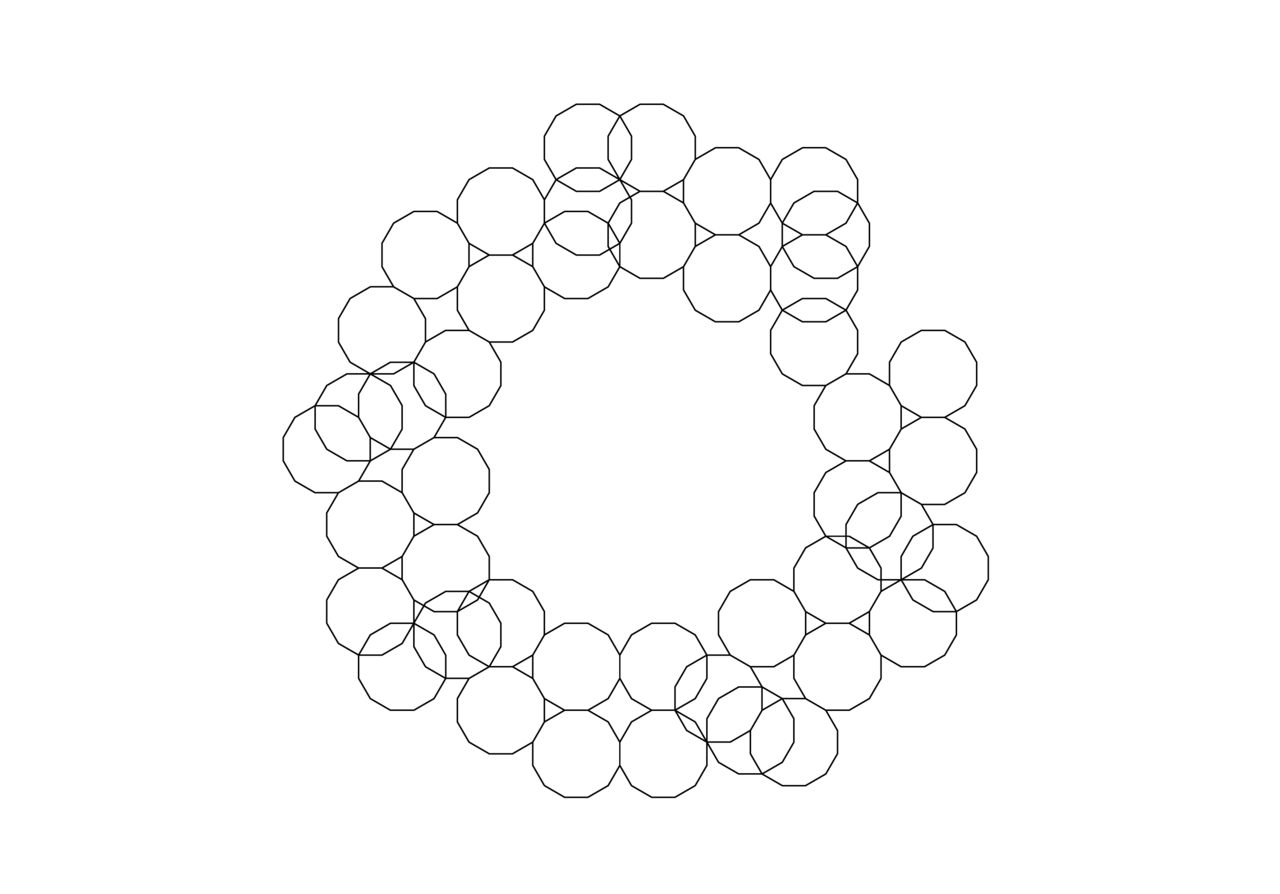


小学生でもできる 東京のエンブレムのつくりかた Takuma Note
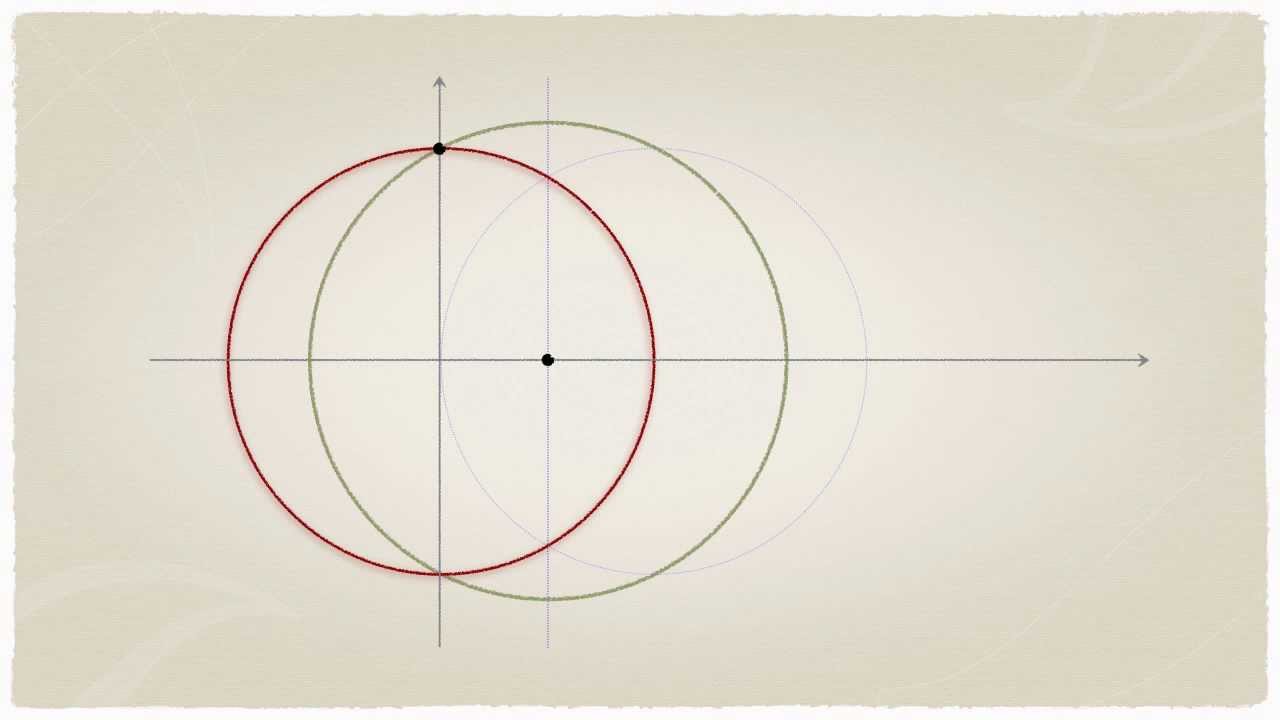
円を使った正六角形のかき方 円中心のまわりを6等分して、 60度になるように半径を順にかきます ※分度器の使い方 ↓ 次にそのはしの点を直線でつなぐと 正六角形ができます。 同じ方法で、正五角形もかけます 360÷5で中心を72°ずつに 分けましょうまず、12分割してひとつの三角形に注目します。 色のついた部分の面積は、全体が04cm 2 ですから、三角形一個当たり\(04 \div 12 = 167\)cm 2 さらにこれを、下図のように分割すると、相似の小さな三角形と平行四辺形に分けられます。正十七角形 基本的には 正五角形の作図 と全く同じ議論を使いますが,正十七角形の作図法はもっと複雑になります.議論の意味自体がよく分からない場合は, 正五角形の作図 に戻って復習してください.『作図可能である』という性質の一番のポイントは,途中の中間体が二次拡大(二次



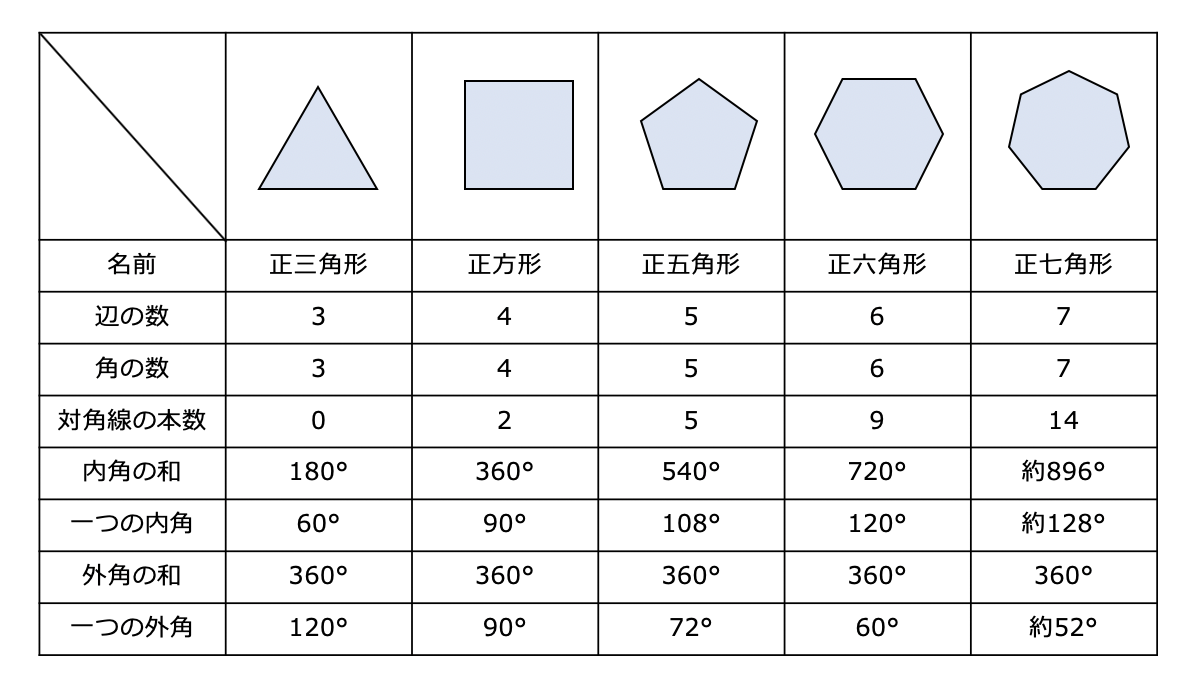
多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典


Cmsweb2 Torikyo Ed Jp T Chu Kyou Shin Action Common Download Main Upload Id 116
180°(122)÷12=150° となります。 〈別解〉 n角形の外角の和は全て360°で一定なので、正n角形の場合、360°をnで割れば一つの外角の大きさが出ます。ひとつの外角の大きさが出れば、それをさらに180°から引いてやればひとつの内角の大きさが出ます。 今回は正12角形なので、多角形の面積 上記のような正12角形の面積を求めよという問題があったとします。 このように一見難しそうな問題であっても、三角比を用いれば簡単に求めることができます。 補助線を引く 以下のように補助線を書き、便宜的に点a、点bを決めます。「正5角形と正面体」 ます。今日の後半は、正多面体をどうやって作るか、その展開図の書き方を考えましょう。 正多面体は、正4面体、立方体、正8面体、正12面体、正面体の5つだけある • ポリドロンの正12面体を見ながら、「正5角形


Http Www2 Hamajima Co Jp Kyoto Math Pdf Kyomath1808 Pdf


Http Math Sakura Ne Jp Action Common Download Main Upload Id 2402
コンパスで正八角形の作図 ってできるんだっけ?? じつはね、 できるんだ。 正八角形の作図は宿題によくでるから、 書き方を知らないと困っちゃうね。 そこで今日は、宿題を瞬殺するために、 正八角形の書き方・作図方法 を5ステップで解説していくよ。正多角形の作図 ガウスは19歳のときに、正n角形がコンパスと定規だけで作図可能であるための条件を与えて、正17角形の作図が可能であることを示し、 数学者になることを決意したそうです。 100角形までの作図可能なものをすべて網羅しました。 正100角形は作図できませんけど。 数学的にどうこうというよりは単にめんどうくさい作業がだらだらつづきます正n角形の1つの内角は、 中1数学 中3数学 161 中学数学二次関数y=ax2のグラフの書き方がわかる3つのステップ



小学校5年 算数 正多角形の角の大きさ Youtube


Www Chofu Schools Jp Kitanodai Sho Tokushoku Documents R1 5nen Sansu Pdf
「正5角形と正面体」 ます。今日の後半は、正多面体をどうやって作るか、その展開図の書き方を考えましょう。 正多面体は、正4面体、立方体、正8面体、正12面体、正面体の5つだけある • ポリドロンの正12面体を見ながら、「正5角形まず初めに、定規で書く正五角形の書き方を紹介します。使用する用具は定規と筆記用具だけという手軽さです。用具がそろっていない場合におすすめです。 書き方の手順<前半> ・手順1:最初に、線分abを引きます。 ・手順2:線分abの中点mをとります。(6) 正7角形を作図する。 付図33 正7角形の作図 補足付図34に示すように,同様の作図法によって,c1=c7,c2=c8,c5=c10,c6=c12となるように点7,点8,点10,点12を求めれば,様々な正多角形を作図できる。ただし,n=6,12以外は近似法である。 付図34 正多角


Http Www2 Hamajima Co Jp Kyoto Math Pdf Kyomath1808 Pdf



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
任意で2点を指定して正五角形を作成しましょう。 ①ポリゴンコマンドを実行します。 今回は、リボンメニューを使用します。 ②コマンドラインに「エッジの数を入力」と表示されますので、正五角形を作成しますので、キーボードから「5」と入力し「Enter」または「Space」で実行をします。 ③コマンドラインに「ポリゴンの中心を指定」と表示されますので計算例 円に外接する正n角形の辺の長さと面積の表を計算します。 円に外接する正多角形 にリンクを張る方法「正5角形と正面体」 ます。今日の後半は、正多面体をどうやって作るか、その展開図の書き方を考えましょう。 正多面体は、正4面体、立方体、正8面体、正12面体、正面体の5つだけある • ポリドロンの正12面体を見ながら、「正5角形


Www Pref Wakayama Lg Jp Prefg Ictforum D Fil Kinokuniict Es Pdf



作図名人への道 正二十面体 受験算数に挑戦
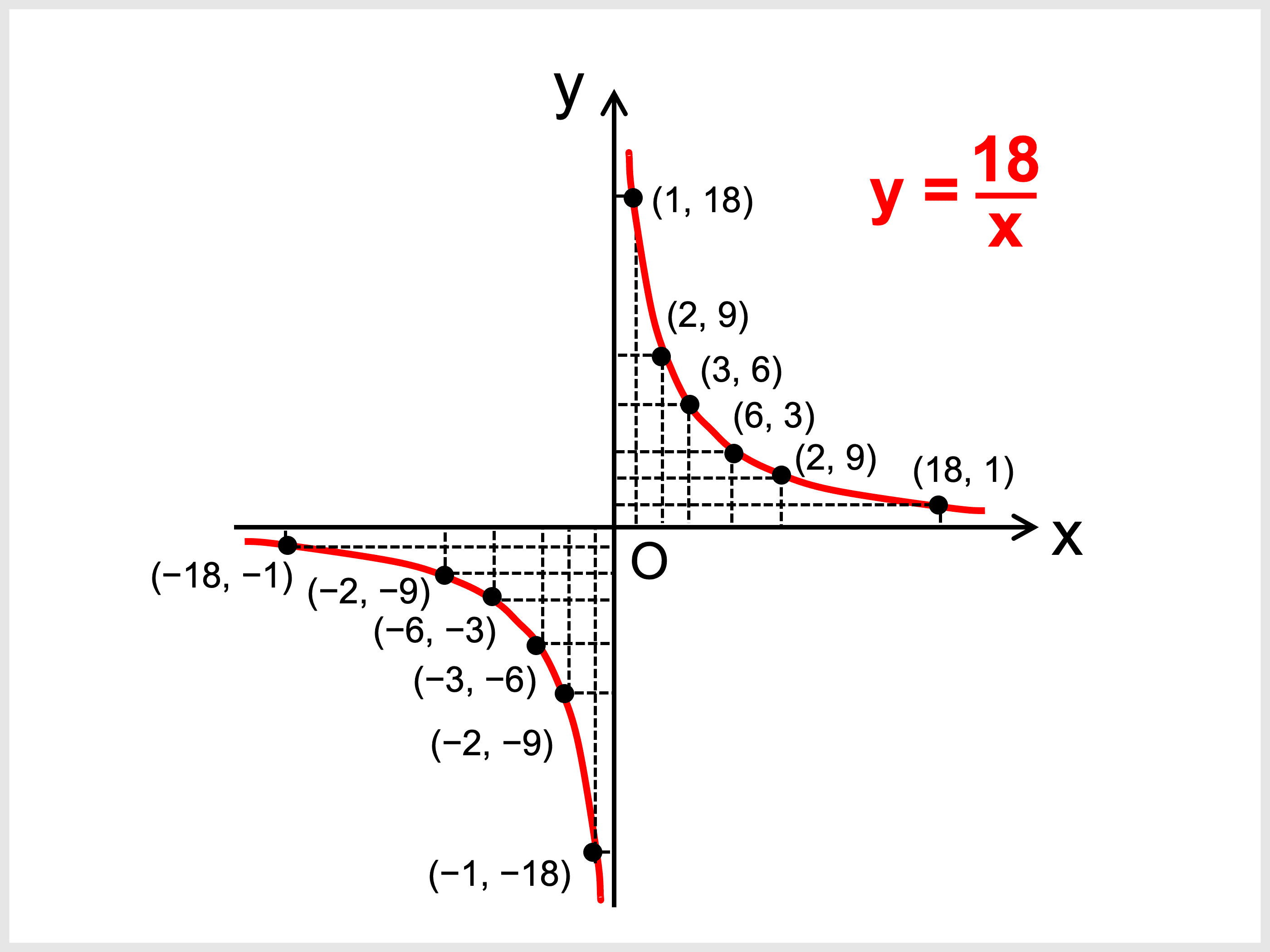


無料でダウンロード 比例 反比例 グラフ リタ ベルナル


Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf


Http Alg Kus Hokkyodai Ac Jp 15 Koshin15aug Pdf



三角比を用いた面積計算をマスターしよう スタディクラブ情報局
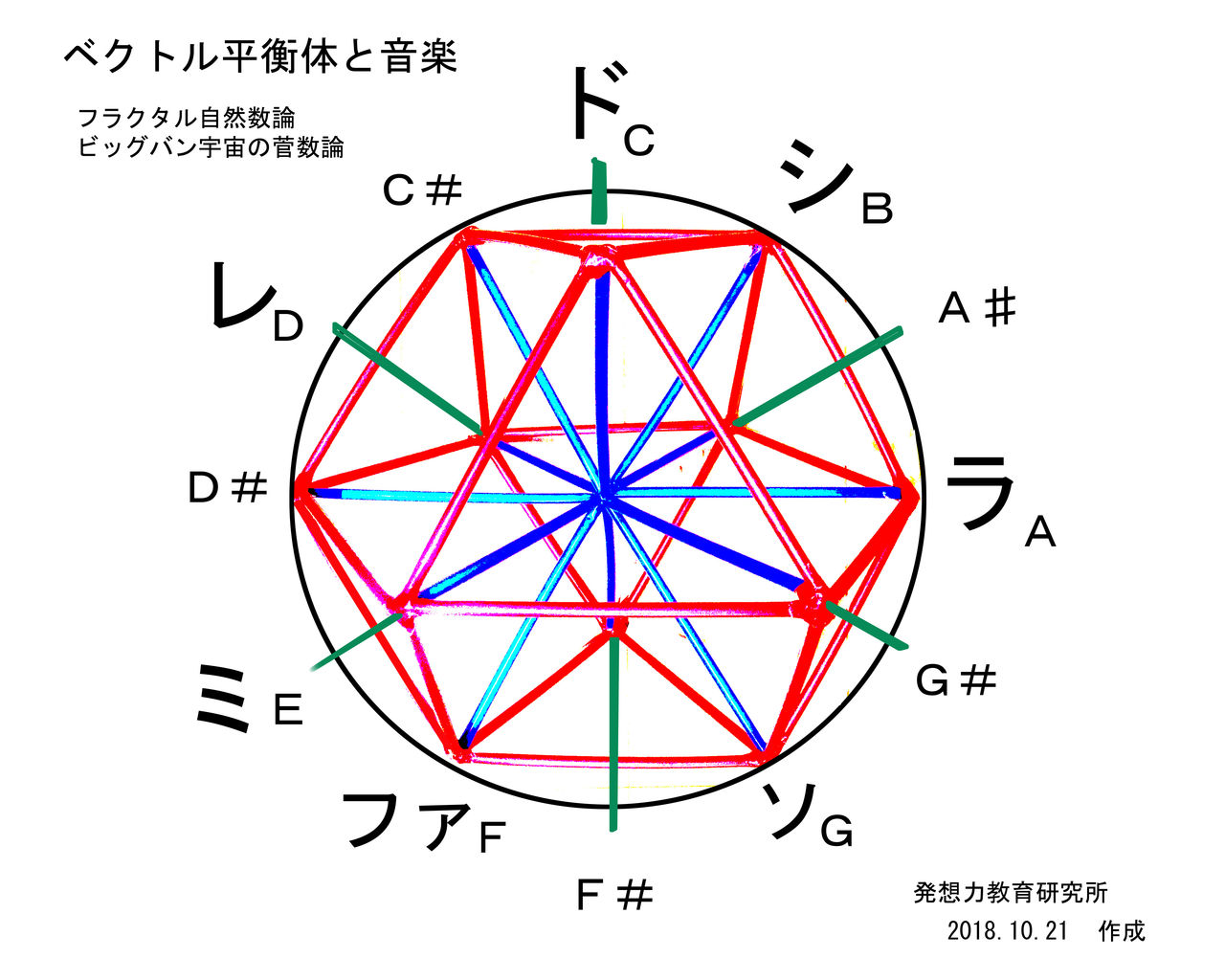


フラクタル自然数1の音楽を見ろ ベクトル平衡体で繋がる数学と音楽と宇宙 発想力教育研究所 素数誕生のメカニズム



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
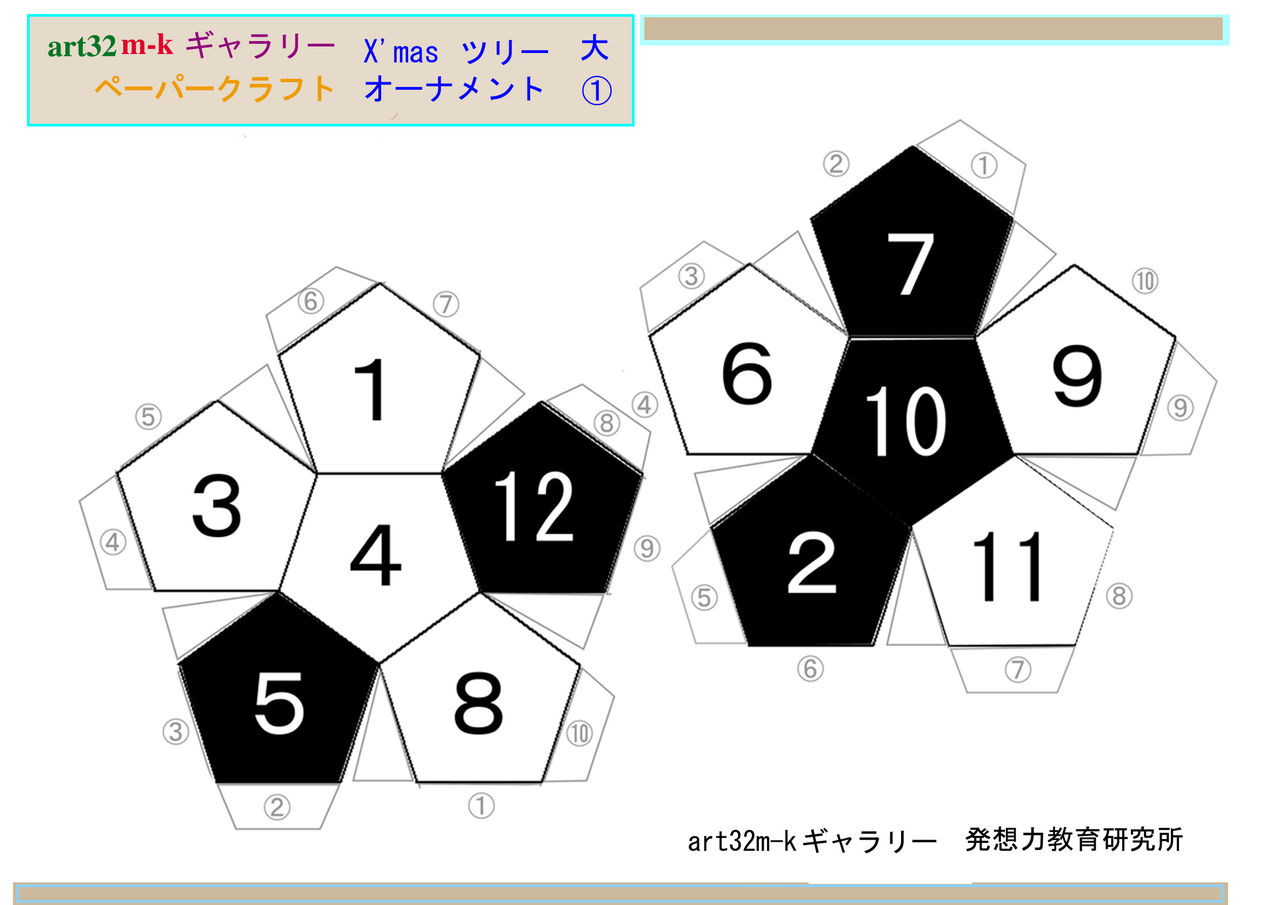


五芒星と二等辺三角形に見る N芒星と正n角形の作図 発想力教育研究所 素数誕生のメカニズム



作図 円に内接する正三角形の作図方法とは 数スタ



空間座標の書き方 Studyaid 編 8 怜悧玲瓏 高校数学を天空から俯瞰する


Http Math Sakura Ne Jp Action Common Download Main Upload Id 2402



難しい多角形を定規だけで描く方法 交点から線で結ぶ Alumania Information



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく


Www Pref Okayama Jp Uploaded Life Misc Pdf


Http Www2 Itc Kansai U Ac Jp Wakui Euler Formula Pdf



星型多角形 Wikipedia


Http Www Kochinet Ed Jp Akidai1 E Kenkyu Tyukanhappyou 5 1 Pdf
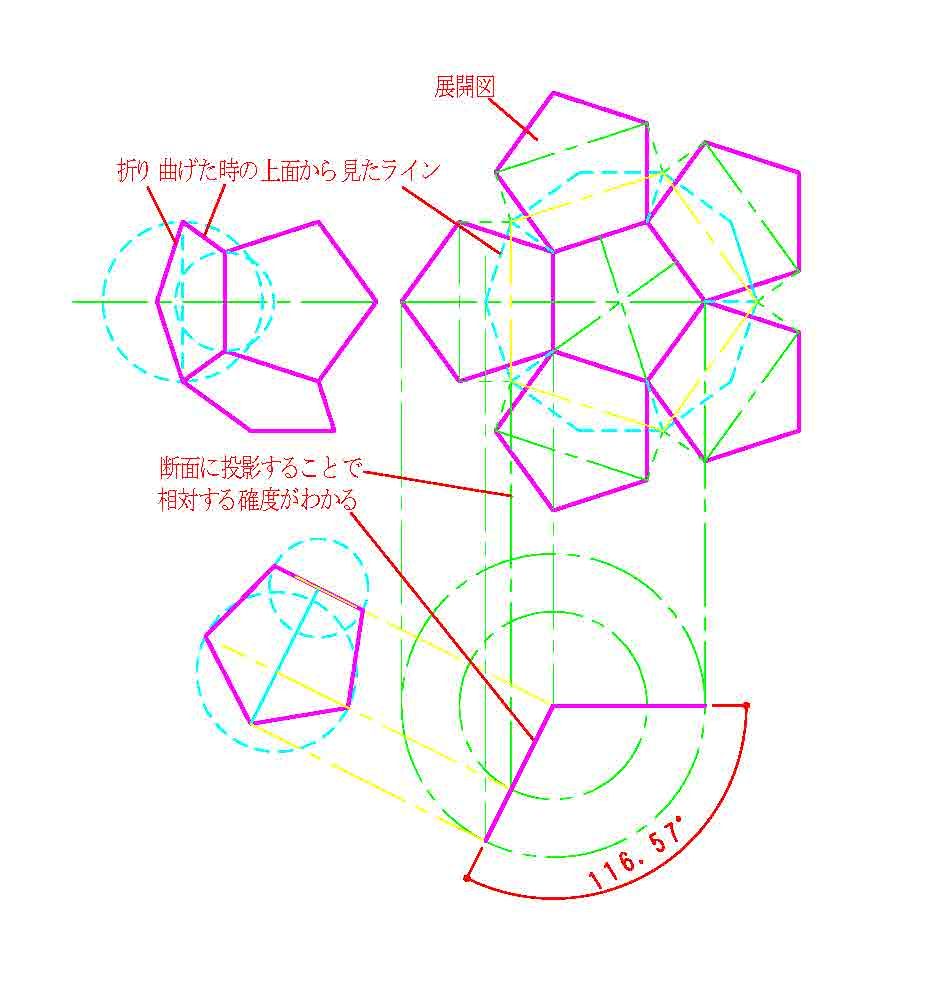


正十二面体のモデリングについて Autodesk Community International Forums


Http Tabunka Or Jp Smd Process Download 1 Download Id 4964


2



十角形 Wikipedia



印刷可能 正12 角形 Hd壁紙画像fhd


Http Www Nc Gunma Boe Gsn Ed Jp Action Common Download Main Upload Id 2719


数学の質問です 1 何人か子供に折り紙を配る 1人に5枚ずつ配 Yahoo 知恵袋



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく


実践例 プログラミングで正多角形を学ぶ 山﨑智仁 Tomohitoy Note



機械設計のための基礎製図


Www Nier Go Jp 12chousa 12mondai Chuu Suugaku B Pdf



75 正 5 角形 の 書き方 壁紙 配布


Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf
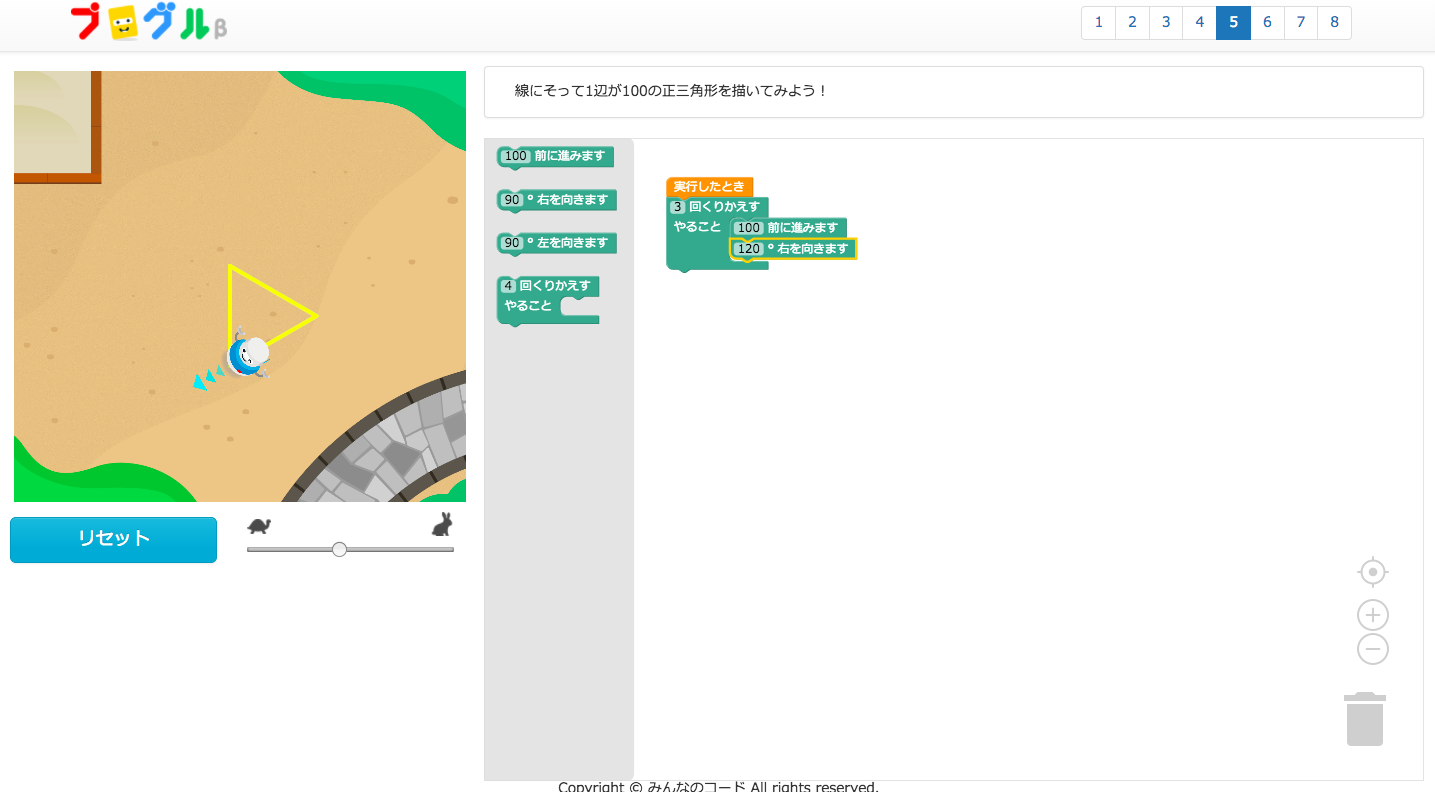


プログラミング教育 算数の指導案 正多角形 プログラミングで 平面図形の理解を深め 算数の深い学びにつなげる
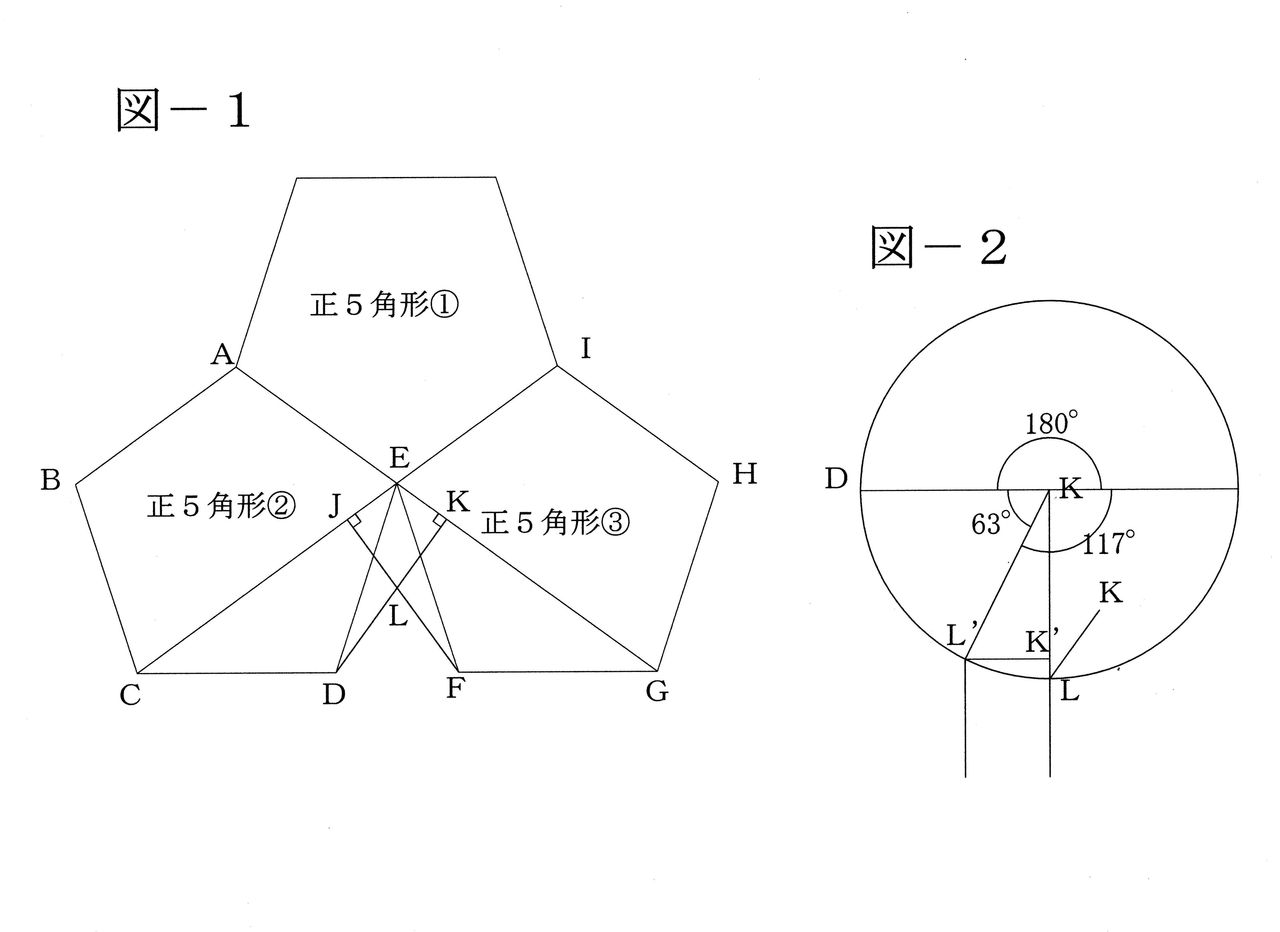


正12面体の内角をcadで求めてみる 自作の友



正二十面体の作成 How To Make Regular Icosahedron Specified By Radius Of Circumscribed Sphere Youtube


第3回 基礎作図 基本的な作図法をしっかりと学ぶ 本日の課題 Ppt Download


Www Chofu Schools Jp Kitanodai Sho Tokushoku Documents R1 5nen Sansu Pdf


Www Chofu Schools Jp Kitanodai Sho Tokushoku Documents R1 5nen Sansu Pdf


Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf


Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf


Www Pref Saitama Lg Jp F2214 Kyouikukatei Documents Sansuu5 Pdf



二十角形 Wikipedia


年 3月 18日 水曜日


第3回 基礎作図 基本的な作図法をしっかりと学ぶ 本日の課題 Ppt Download



高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月


数学の質問です 1 何人か子供に折り紙を配る 1人に5枚ずつ配 Yahoo 知恵袋


Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf


任意の二等辺三角形だけで描き出される正多角形と正多面体を笑えるか 発想力教育研究所 素数誕生のメカニズム



アルキメデス以来の新種発見 正七角形を使った半正多面体 発想力教育研究所 素数誕生のメカニズム



九角形 Wikipedia


Http Math Sakura Ne Jp Action Common Download Main Upload Id 2402



フリーハンドで正十二面体 多面体 を描く その方法をご紹介します 数学 幾何学 Mathematics Youtube


正五角形の作図法 ガロア理論 Youtube



第3回 基礎作図 基本的な作図法をしっかりと学ぶ 本日の課題 Ppt Download



星形の角度 内角の和の求め方を問題解説 数スタ


二角形 Digon Japaneseclass Jp



二百五十七角形 Wikipedia


2


Www Mext Go Jp B Menu Shingi Chukyo Chukyo3 004 Siryo Icsfiles Afieldfile 18 10 05 7 Pdf


2



算数 53 正十二角形の面積 城北 平面図形 Youtube



ガウスが見つけたという定規とコンパスだけの正17角形の作図 Gifアニメになってたのか Fallen Physicist Rising Engineer


小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報



正十二角形 Youtube



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



難しい多角形を定規だけで描く方法 交点から線で結ぶ Alumania Information


Http Math Sakura Ne Jp Action Common Download Main Upload Id 2402



十二芒星 Wikipedia


九角形 Wikipedia



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



75 正12角形 子供向けぬりえ


Http Www Ms U Tokyo Ac Jp Tambara Docs C4jh10 1tsuboi Pdf



任意の二等辺三角形だけで描き出される正多角形と正多面体を笑えるか 発想力教育研究所 素数誕生のメカニズム



十九角形 Wikipedia



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



十七角形 Wikipedia



難しい多角形を定規だけで描く方法 交点から線で結ぶ Alumania Information


Http Www2 Hamajima Co Jp Kyoto Math Pdf Kyomath1808 Pdf
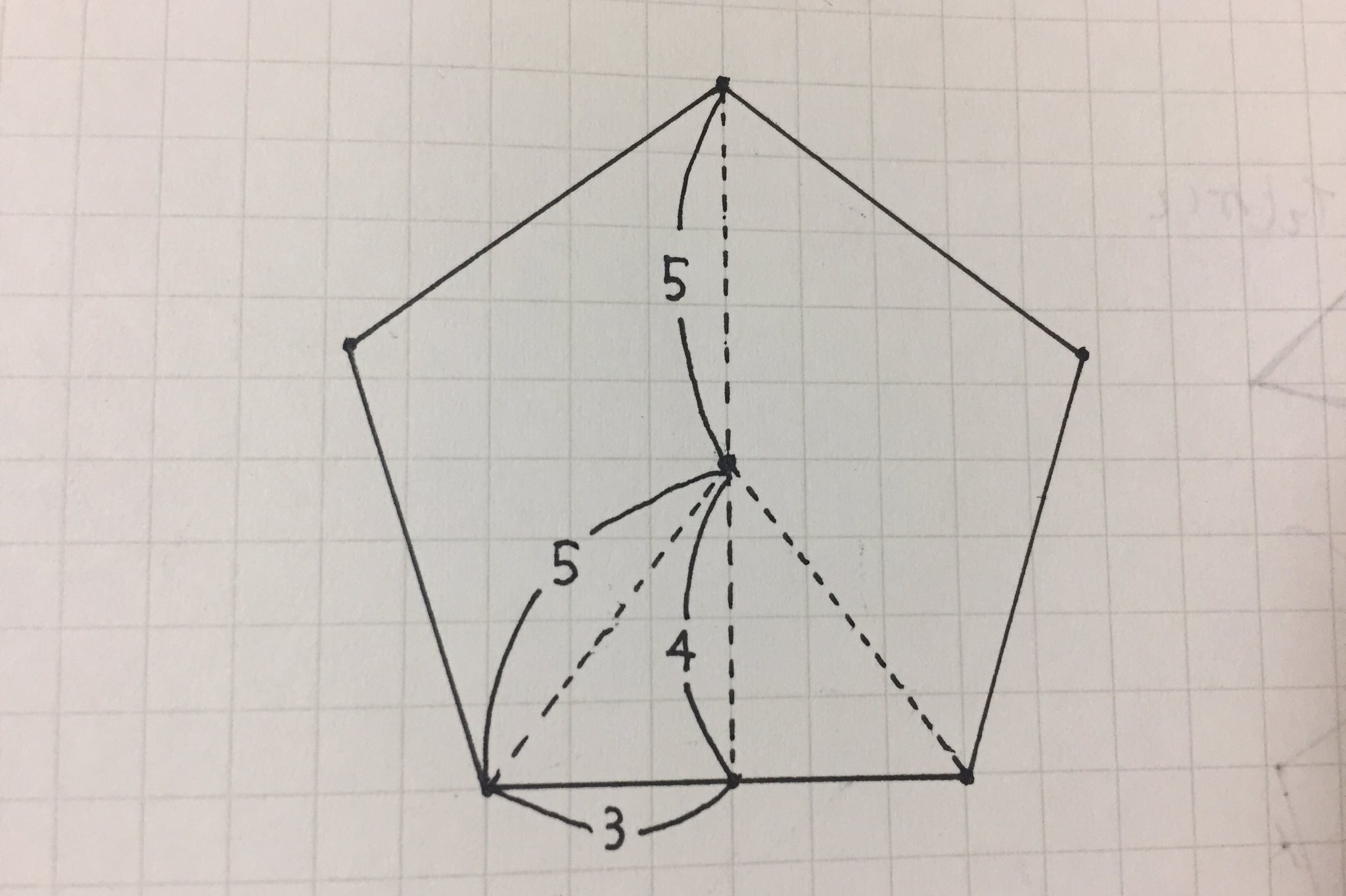


Askaboutmathp 方眼紙のマス目をいかして ほぼ 正五角形を描く描き方を考える過程で面白い事実に気づきました 中心点と頂点を結んでできる三角形は ほぼ ピタゴラスの三角形 3 4 5 を2つ組み合わせた形になります 今まで全く気が付きませんでした 意外な


Http Www2 Hamajima Co Jp Kyoto Math Pdf Kyomath1808 Pdf



十二角形 Dodecagon Japaneseclass Jp



難しい多角形を定規だけで描く方法 交点から線で結ぶ Alumania Information


2


Http Ousar Lib Okayama U Ac Jp Files Public 5 Papyrus 001 055 061 Pdf



十二角形 Wikipedia



中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく


Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf



十六角形 Wikipedia



75 正12角形 子供向けぬりえ



0 件のコメント:
コメントを投稿